算法—矩阵连乘
算法描述
【问题描述】
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。现在需要研究的问题是如何确定矩阵连乘积的计算次序,使得计算矩阵连乘所需的乘法次数最少。
矩阵连乘问题满足结合律, 其计算次序可以用加括号的方式确定,若矩阵连乘已完全加括号,则其计算次序完全确定。例如,有四个矩阵A,B,C,D,它们的维数分别是:A=50×10,B=10×40, C=40×30, D=30×5。ABCD矩阵连乘共有五种完全加括号的方式,计算次序和乘法次数如下:
(A((BC)D)) 16000 (A(B(CD))) 10500
((AB)(CD)) 36000 (((AB)C)D) 87500
((A(BC))D) 34500
可见不同的计算次序会导致不同的计算代价,我们要做的就是让计算代价最小。
【输入】第1行输入连乘矩阵的个数n,第2行依次输入连乘矩阵的大小。
【输出】输出包括两行,第1行输出最小的计算量,第2行输出矩阵连乘完全加括号的形式。
【输入样例1】
4
50 10 40 30 5
【输出样例1】
1050
(A1)
【输入样例2】
3
5 6 3 4
【输出样例2】
150
((A[1]A[2])A[3])
C语言实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include<stdio.h>
int N;
int p[100],m[100][100],s[100][100];
int MatrixChain(int *p,int n){
for(int i=1;i<=n;i++)
m[i][i]=0;
for(int r=2;r<=n;r++){
for(int i=1;i<=n-r+1;i++){
int j=i+(r-1);
m[i][j]=m[i][i]+m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
for(int k=i+1;k<j;k++){
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t<m[i][j]){
m[i][j]=t;
s[i][j]=k;
}
}
}
}
return 0;
}
void Traceback(int i,int j){
if(i==j)
{
printf("A%d",i);
}
else
{
printf("(");
Traceback(i,s[i][j]);
Traceback(s[i][j]+1,j);
printf(")");
}
}
int main(){
printf("请输入矩阵数量:");
scanf("%d",&N);
N=N+1;
printf("请输入各矩阵纬度(用空格分隔):");
for(int i=0;i<N;i++)
scanf("%d",&p[i]);
MatrixChain(p,N-1);
Traceback(1,N-1);
printf("\n");
return 0;
}
|
运行截图
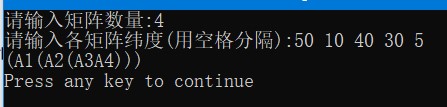
运行截图示例1

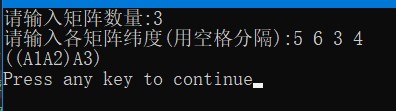
运行截图示例2