贪婪算法之背包问题
算法描述
设有编号为1、2、…、n的n个物品,它们的重量分别为w1、w2、…、wn,价值分别为v1、v2、…、vn,其中wi、vi(1≤i≤n)均为正数。
有一个背包可以携带的最大重量不超过W。求解目标:在不超过背包负重的前提下,使背包装入的总价值最大(即效益最大化),与0/1背包问题的区别是,这里的每个物品可以取一部分装入背包。
C语言的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<stdio.h>
#define MAX 101
void sort(int n,float w[],float v[]){
int i,j;
float temp1,temp2;
for(i=1;i<=n;i++)
for(j=1;j<=n-i;j++)
{
temp1=v[j]/w[j];
temp2=v[j+1]/w[j+1];
if(temp1<temp2)
{
float temp;
temp=w[j];
w[j]=w[j+1];
w[j+1]=temp;
temp=v[j];
v[j]=v[j+1];
v[j+1]=temp;
}
}
}
int main(){
float p[MAX],w[MAX],v[MAX];
int n;
float M;
printf("请输入物品总数n和背包最大容纳重量M:");
scanf("%d %f",&n,&M);
for(int i=1;i<=n;i++)
{
printf("请输入第%d件物品的重量和价值:",i);
scanf("%f %f",&w[i],&v[i]);
}
sort(n,w,v);
float c=M;
for(i=1;i<=n;i++)
{
p[i]=0;
}
for(i=1;i<=n;i++)
{
if(c>=w[i])
{
p[i]=1;
c=c-w[i];
}
else
{
p[i]=c/w[i];
break;
}
}
for(i=1;i<=n;i++)
{
printf("重量为%.0f,价值量为%.0f,的物品,放入的比例为%.2f\n",w[i],v[i],p[i]);
}
return 0;
}
|
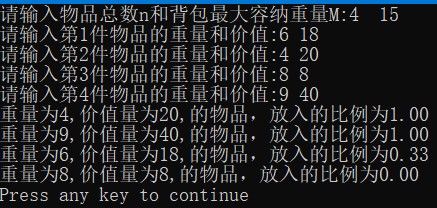
运行截图