动态规划算法求数塔问题
算法描述
【实验目的】
1.掌握动态算法的思想和求解问题的步骤;
2.用动态规划算法策略求解数塔问题;
3.用动态规划算法策略求解收获花生问题。
【实验内容】
1.动态规划算法求解数塔问题
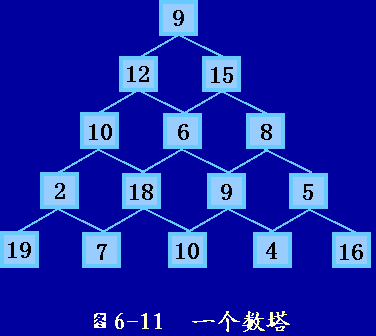
【问题描述】数塔问题
有如下图所示的一个数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的数值和最大。

【算法设计】给出算法设计思想,并用动态规划算法实现。
C语言的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include<stdio.h>
#define MAX 1000
int data[MAX][MAX];
int dp[MAX][MAX];
int n;
void tower_walk(){
for(int i=1;i<=n;i++)
{
dp[n][i]=data[n][i];
}
int temp_max;
for(i=n;i>=1;i--)
{
for(int j=1;j<=i;j++)
{
if(dp[i+1][j]>dp[i+1][j+1])
temp_max=dp[i+1][j];
else if(dp[i+1][j]<dp[i+1][j+1])
temp_max=dp[i+1][j+1];
else
temp_max=dp[i+1][j];
// temp_max=max(dp[i+1][j],dp[i+1][j+1]);
dp[i][j]=temp_max+data[i][j];
}
}
}
int print_tower(){
printf("最大路径和是:%d\n",dp[1][1]);
int node_value;
printf("最大路径是:%d",data[1][1]);
int j=1;
for(int i=2;i<=n;i++)
{
node_value=dp[i-1][j]-data[i-1][j];
if(node_value==dp[i][j+1])
++j;
printf("-->%d",data[i][j]);
}
printf("\n");
return 0;
}
int main(){
printf("请输入塔的层数n:");
scanf("%d",&n);
printf("请输入塔每个节点的数据(第i层有i个节点):\n");
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
scanf("%d",&data[i][j]);
}
}
tower_walk();
print_tower();
return 0;
}
|
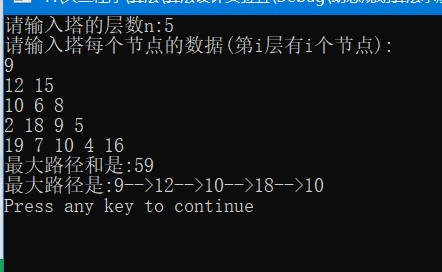
运行截图