动态规划算法求最大子段和
问题描述
【问题描述】
给定由n个整数组成的序列a1,a2,…,an,求该序列子段和的最大值。当所有整数均为负值时定义其最大子段和为0。
依此定义, 例如, 当(a1,a2, a3, a4, a5,a6)=(-2, 11, -4, 13, -5, -2)时,最大子段和为20。
【问题分析】

【算法设计】
给出算法设计思想,并用动态规划算法实现。
C语言的实现
1 | #include<stdio.h> |
运行截图
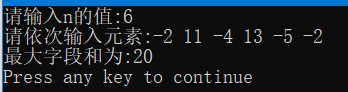
【问题描述】
给定由n个整数组成的序列a1,a2,…,an,求该序列子段和的最大值。当所有整数均为负值时定义其最大子段和为0。
依此定义, 例如, 当(a1,a2, a3, a4, a5,a6)=(-2, 11, -4, 13, -5, -2)时,最大子段和为20。
【问题分析】

【算法设计】
给出算法设计思想,并用动态规划算法实现。
1 | #include<stdio.h> |
